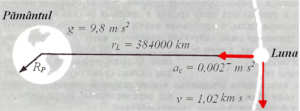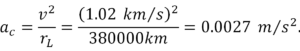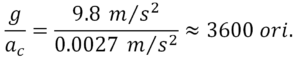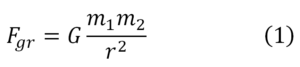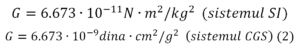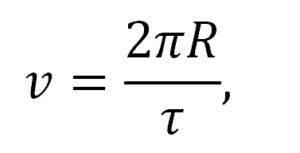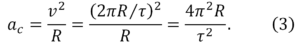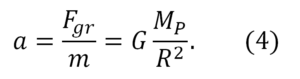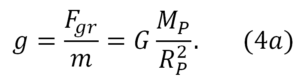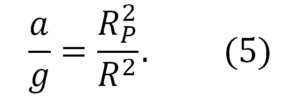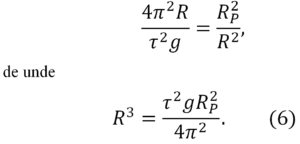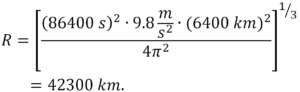Forțele fundamentale în natură. Interacțiunea gravitațională

În experiența zilnică noi ne întâlnim cu diverse forțe. Pentru a deschide ușa, trebuie de aplicat forța musculară și de învins forța de frecare în bălămălile ușii și forța elastică din resortul ușii. Noi observăm forțele, cu care atmosfera apasă asupra barometrului și Pământului acționează asupra Lunei. Forța electrică pornește motorul automobilului, hidraulică lucrează în frânele lui, iar dacă nu i-a mers și a tamponat un felinar, atunci oprirea sa se datorează forței mecanice. Însă, necătând la diversitatea denumirilor, pe care noi le dăm forțelor utile și nocive, există doar două tipuri de bază a forțelor, care dirijează comportarea obiectelor în viața cotidiană, forțele gravitaținale și electrastatice (interacțiunile). Toate forțele menționate mai sus sunt manifestările acestor două interacțiuni fundamentale.

În articolul de față noi detaliat vom analiza interacțiunele gravitaționale și acelea interacțiuni electrice, care există, când sarcinile se află în repas, adică forțele electrostatice. Interacțiunile numite, însă, sunt insuficiente pentru descrierea fenomenelor nucleare. Cercetarea proceselor cu participarea nucleelor și particulelor elementare a arătat, că în natură există interacțiuni încă de două tipuri așa numitele puternice, sau nucleare și slabe. Interacțiunile gravitaționale și electrostatice sunt de acțiune îndepărtată (adică acțiunea lor este observată la distanțe mari). Anume din acestă cauză ele sunt răspunzătoare de toate fenomenele pe scară largă, macroscopice – începând cu fenomenele din viața cotidiană și finisând cu acelea ce au loc în stelele și galaxiile îndepărtate. Interacțiunele nucleare și slabe au loc o rază de acțiune foarte scurtă, de aceea fenomenele cauzate de ele sunt observabile doar în scara dimensiunilor nucleare. Necătând la aceasta forțele date joacă un rol premordial pentru existența noastră. Viața pe Pământ este susținută datorită luminii solare, iar ea însuși este produsul final al proceselor nucleare, ce au loc în adâncimea Soarelui.

În așa fel, nici una din cele patru interacțiuni menționate nu este de prisos. Toate ele în mod egal sunt necesare pentru ”funcționarea normală” a Universului. Evident nu putem exclude faptul, că natura este constituită mai complicat, decât noi credem, însă în ziua de azi noi cunoaștem patru tipuri de forțe sau interacțiuni – gravitaționale, electrice, puternice și slabe. Procesele care noi le observăm, după toate nu necesită atragerea încă cărorva tipuri de forțe. Este curios, că natura a fost în stare să construiască tot Universul, utilizând doar patru tipuri de forțe fundamentale.

Interacțiunea gravitațională

Calculele lui Newton. Noi cunoaștem, că mișcarea accelerată a corpului apare doar la acțiunea unei forțe aplicate lui. Forța gravitațională (forța de greutate) impune accelerația de 9.8 m/s² corpurilor, în căderea liberă la suprafața Pământului. Această forță acționează pe Pământ, însă noi putem pune întrebarea: este oare Pământul unicul loc unde există forța de greutate sau această forță acționează în întregul Univers? Întrebarea analogă a apărut la Newton, însă el nu dispunea de mijloace pentru clarificarea în ce măsură este universală atracția, măcăr în afara Sistemului Solar. De aceea Newton a ales pentru cercetare sistemul Pământ – Lună. El a presupus, că forța ce menține Luna pe orbită lângă Pământ, este aceeași forță, care atrage corpurile în apropierea suprafeței Pământului. Din măsurările triangulare efectuate până la el Newton cunoștea, că distanța de la Pământ până la Lună r_L aproximativ de 60 de ori depășește raza Pământului R_P, care aproximativ este egală cu 6400 km (fig. 1), de unde r_L~ 380000 km. Newton la fel cunoștea perioada de rotație a Lunei în jurul Pământului t = 27.3 zile. Pentru menținerea mișcării pe orbită Luna trebuia să suporte o accelerație centripetă egală cu raportul pătratului vitezei liniare la raza orbitei, a_c = v²/r_L. Viteza liniară a Lunei:

Fig. 1 Accelerația centripetă al Lunei condiționată de atracția gravitațională a Pământului.

Reese, accelerația centripetă a Lunei

Această accelerație este mai mică de accelerația forței gravitaționale g pe suprafața Pământului de

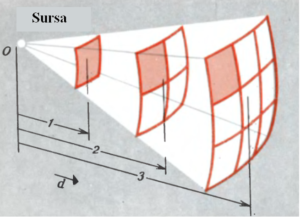
Legea conform căreia se micșorează o oarecare mărime la distribuirea ei izotropă în spațiu fără absorbție (de exemplu lumina vezi fig.2), – este legea proporționalității inverse a pătratului distanței, adică 1/r².

Fig. 2 Intensitatea luminii, uniform radiată de sursă în toate direcțiile, se micșorează cu distanța până la sursă d după relația 1/d².

Newton a presupus, că forța gravitațională, la fel ca iluminarea, se micșorează proporțional cu pătratul distanței. De aceea, dacă Luna se află de la centrul Pământului de 60 de ori mai departe, decât corpul aflat pe suprafața Pământului, atunci forța gravitațională și accelerația pentru Lună trebuie să fie mai mică de (60)² ori, adică de 3600 ori. Anume această valoare are raportul g/a_c.

Măcăr că valoarea calculată și observată au coincis, astfel justificând ipoteza lui Newton, trebuie de atras atenția la două momente:

Newton a considerat, că forța gravitațională este invers proporțională pătratului distanței dintre corpurile ce interacționează. Această presupunere a dat un rezultat corect pentru sistemul Pământ – Lună, însă nu erau garanții, că ea va fi justă și pentru alte sisteme cu alte distanțe între corpuri. Newton a aplicat presupunerea despre legea la mișcarea altor planete – satelite ale Soarelui și a găsit, că ea la fel se respectă. Mai târziu s-a clarificat, că legii gravitaționale a lui Newton se supun și stele duble (adică două stele ce se rotesc una în jurul alteia). De aceea este foarte probabil, că forța gravitațională variază conform legii în întreg Univers. Până când nu s-au putut găsi excepții din această lege (însă vezi, observațiile care vor fi indicate în articolele următoare).
La potrivirea valorii accelerației centripete a Lunei a_c cu valoarea g ambele distanțe s-au considerat de la centrul Pământului. Când Newton efectua calculele sale (în anul 1666), el nu a putut argumenta alegerea sa a punctului de referință și sa obținut atunci de la publicarea rezultatelor obținute de el. Legea newtoniană a atracției Universale a văzut lumina numai în anul 1687, după ce Newton a elaborat aparatul matemtic (calculul diferențial), ce i-a permis să fundamenteze calculele efectuate anterior. Cu ajutorul acestui aparat Newton a reușit să demonstreze, că dacă masa fiecărui din două corpuri omogene de formă sferciă de considerat concentrată în centrul corpului, atunci corpurile se vor atrage unul spre altul cu forța, ce variază conform legii 1/r². Acest rezultat important a devenit cheia către legea atracției: el a permis de efectuat toate calculele forțelor gravitaționale, considerând, că masa corpurilor de formă sferică, – iar aceasta este forma Pământului și a Lunei, – sunt concentrate în centrul lor.

Fig. 3 Concentrație sferică de stele în constelația Hercule.

Atracția a concis în această aglomerație sute de mii de stele. Richard Feynman, laureat premiului Nobel la fizică în anul 1965, a spus, că ”trebuie să fii lipsit de imaginație, ca să nu observi aici efortul atracției”.

LEGEA ATRACȚIEI UNIVERSALE

Rezultatul obținut de Newton, se exprimă prin următoarea lege: forța gravitațională, cu care se atrag reciproc două particule (sau două corpuri de formă sferică), este invers proporțională cu pătratul distanței dintre centrele lor și este direct proporțională cu produsul maselor lor:

unde termenul de proporționalitate G se numește constanta gravitațională. Valoarea G este egală

SATELIȚII ARTEFICIALI GEOSTAȚIONARI AI PĂMÂNTULUI

Una din cele mai importante atingiri din ultimul timp în domeniul comunicațiilor este crearea sistemului de sateleți arteficiali ale Pământului, care nemișcat atârnă deasupra a unor anumite puncte ale ecuatorului Pământesc. Astfel de sateliți arteficiali poartă aparataj de retranslare, ce permite instalarea unui multi-canal de comunicare între continente (fig. 4).

Fig. 4 Sateliții arteficiali permit de obținut legătură UUS – radio (unde ultra scurte) între punctele îndepărtate a suprafeței pământești.

Fără sateliți o astfel de comunicare este imposibilă, deoarece undele radio se propoagă în limitele vizibilității drepte.

Înălțimea la care trebuie să se afle orbita unor astfel de sateliți, se determină de faptul, că perioada de rotație sateliților trebuie exact să coincidă cu perioada de rotație al Pământului în jurul axei proprii. La o așa de condiție Pământul și satelitul se vor roti cu o aceeași viteză unghiulară, și satelitul va ocupă o poziției constantă (staționară) relativ de Pământ.

Viteza liniară al satelitului depinde de distanța până la centrul Pământului conform formulei